Lämpöakun simulointi

Lämpöakun rakenne

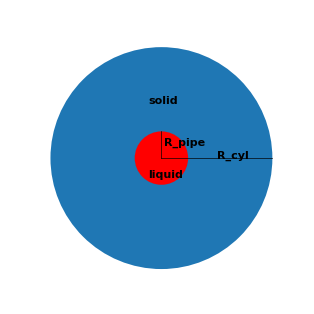
Lämpöakussa lämpöä varastoidaan kiinteään aineeseen, jonka läpi pumpataan nestemäistä lämmönsiirtoainetta.

Simulointi yksinkertaistuu merkittävästi, jos oletamme lämpövaraston sylinteriksi, koska symmetrian ansiosta sylinterin kuvaamiseen riittää kaksi koordinaattia l ja r. Kolmiulotteinen ongelma pelkistyy kaksiulotteiseksi.

longitudal — Sylinterin pitkittäisleikkaus

Muutama esimerkki simuloinnin tuloksista

(Videot eivät ehkä aukea linkistä klikkaamalla, koska selaimet eivät aina ymmärrä paikallisia tiedostoja. Aukevat klikkaamalla tiedostoa hakemistotyökalullasi. Ellei onnistu, installoi VideoLAN VLC media player. )

Suureita ajan funktiona, sylinteri 20cm

Suureita ajan funktiona, sylinteri 30cm

erotus 20cm - 30cm

Huitaistu alustava tarkastelu:

Kummassakin ajossa on käytetty samaa maksimitehoa. Paksumpi sylinteri vastaanottaa lämpöä paremmin, joten öljy jäähtyy niin paljon, ettei lämmitin kykene lämmittämään öljyä maksimilämpöön. Lämpöä varastoituu sylinteriin jokseenkin sama määrä, mutta paksumpi sylinteri jää kylmemmäksi, minkä takia siitä ei saada yhtä pitkää aikaa maksimilämpöistä öljyä ulos.

Simulointi

Parametrit

Simuloinnin parametrit syötetään tiedostoon:

Sylinterin dimensiot,
materiaalien ominaisuudet,
moneenko osaan sylinteri jaetaan radiaali- ja pituussuunnassa (putki vain pituussuunnassa)
Ohjausalgoritmin parametrit

# Parameters for heat storage simulation

geometry:
  L: 160.0  # Length of cylinder [m]
  R_solid: 0.2 # Outer radius of cylinder [m]
  R_pipe: 0.048  # 0.074 Radius of pipe [m]

Virtauksen nopeus vaikuttaa lämmönsiirtoon ja simuloinnin aika-askeleeseen. Ohjelmassa olevan tarkistuksen mukaan 0.5 m/s on vielä turbulenttinen nykyisellä putkikoolla.

0.5 m/s nopeuttaa testiajoja, mutta lämmönsiirto on on heikompaa kuin nopeammalla virtauksella. Vakavat tarkastelut pitää tehdä todellisella virtausnopeudella

Algoritmi olettaa virtausnopeuden vakioksi. Algoritmia pitää täydentää, mikäli nopeutta halutaan vaihdella simuloinnin aikana


fluid:
  v: 0.5                 # m/s
  rho: 920.0        # Density kg/m^3
  cp: 2200.0        # Specific heat J/(kg·K)
  k: 0.12              # Thermal conductivityW/(m·K)
  nu: 4.0e-6        # 5.0e-6  Kinematic viscosity m^2/s
  # !!!kinematic viscosity typically decreases when temperature increases. Not implemented yet

solid:
  rho: 2300.0 # Density kg/m^3
  cp: 1000.0 # Specific heat J/(kg·K)
  k: 1.0 # Thermal conductivityW/(m·K)

Diskretointi, laskentahilan tiheys. vaikuttavaa laskennan tarkkuuteen.

Nz_solid, pituussuuntainen diskretointi, vaikuttaa paljon laskenta-aikaan, koska se määrittää simuloinnissa käytettävän aika-askeleen: Yhdessä aika-askeleessa neste saa edetä vähemmän kuin yhden "siivun" mittaisen matkan. Muutoin muutokset nesteen lämpötilassa eivät ehtisi vaikuttaa kaikkiin sylinterin osiin

Nr_solid "kerrosta" säteen suunnassa
Nz_solid "siivua" pitkittäissuunnassa

Putki jaetaan yhtä moneen "siivuun" kuin kiinteä sylinteri

Putkea, nestettä, ei jaeta säteen suunnassa osiin vaan luotetaan yleisesti käytettyihin approksimaatioihin


mesh:
  Nr_solid: 60
  Nz_solid: 100
  # Nz_fluid: set automatically to Nz_solid

grad määrittää, kuinka paljon tiheämpi hila on lähellä putkea, jossa on suurimmat lämpötilaerot ja vähemmän lämpöä vastaanottavaa massaa.

bump määrittää, paljonko tiheämpi hila on sylinterin/putken päissä keskikohtaan verrattuna


grad: 2.6  # 1.2 - 3, smaller is milder
bump: 0.3 # 0.2 - 0.5, bigger is milder

Jäähdytettäessä nesteen lämpötila lasketaan alimmillaan T_cold:iin

T_hot on nesteen ylin sallittu lämpötila.

Simulointi aloitetaan lämpötilasta T_initial (sekä sylinteri että neste)


operating_conditions:
T_cold: 293.15  # Cold temperature [K]
T_hot: 698.15  # Hot temperature [K]
T_initial: 293.15  # Initial temperature [K]

Kun tehdään askelmainen muutos lämmitys- tai jäähdytystehossa, akkuun menevän nesteen lämpötila nousee pehmeästi ajassa tau_heater.

dT_min ja dT_max ovat maksimi lämpötilaero, minkä lämmitin/jäähdytin kykenee tuottamaan. Loppukäyttäjää ajatellen tähän pitää laittaa tehot ja laskea nämä tehoista


controller_parameters:
tau_heater: 600 # [s] rise time of input temperature,

dT_max: 60.0
dT_min: -30.0

Simulointiajon vaiheet. Näitä voi laittaa peräkkäin tarpeen mukaan. Kesto ilmoitetaan tunteina.


  phases: [     # charge, discharge, steady
    {"type": "charge", "duration": 8.0},
    #{"type": "steady", "duration": 0.25},
    {"type": "discharge", "duration": 16.0}
    ]

convective heat transfer coefficient, usually denoted h and expressed in units of W/(m²·K).


htc:
  h: null           # null -> compute via Gnielinski once; set a number to override

Kun CFL < 1, virtaus putkessa ei "ohita" yhtään laskentahilan "siivua".


numerics:

  cfl_target: 0.8 # < 1.0
  dt: null         # null -> pick from CFL

Temppu, jolla voi pyöristää nesteen lämpötilan nopeita muutoksia, jotka muuten tekisivät numeerisesta ratkaisusta epätarkan.

Simuloinnissa jäähdytin/lämmitin on mallinnettu "hitaaksi", koska käytännössä on mahdoton saada aikaiseksi suuria askelmaisia lämpötilan muutoksia, joten tällainen epäfysikaalinen temppu on turha ja pitkässä putkessa aiheuttaisi virhettä.


alpha_f: 0.0     # 0.1 - 0.3 axial diffusion, artificial

Generoitavan videon haluttu pituus. Mitä pidempi, sitä tiuhemmassa aikapisteitä. Tähän voisi lisätä mahdollisuuden ilmoittaa, montako framea sekunnissa video näyttää. 96 frame/s tuplaa nopeuden verrattuna 48 frame/s. Standardi taitaa olla 30 frame/s.


animation:
  #
  video_duration: 1.0 # [minutes] videon kesto (48 kuvaa/s)

Ohjausalgoritmi

Ohjausalgoritmi suorittaa sarjan lataus-, purku- ja tyhjäkäynti-vaiheita. Kunkin vaiheen pituus määritetään tunteina.

Akkuun pumpattavan nesteen lämmityksen ja jäähdytyksen teholle asetetaan maksimiarvo (Tällä hetkellä parametreissä dT_max ja dT_min, kuten yllä selitettiin). Ohjausalgoritmi pitää tehon maksimi- tai minimiarvossa, ellei öljyn lämpötila ylitä/alita sallittua.

Jäähdytys ja lämmitys -elementti on mallinnettu 2-asteen prosessilla niin, että tehon asetusarvon askelmainen muutos näkyy elementin ulostulon lämpötilassa pehmeästi. Numeerinen ratkaisu helpottuu, kun ei tarvitse varautua lämpötilan hyppäyksiin, jollaisia ei kuitenkaan voi todellisuudessa tapahtua.

Simuloinnin mahdollisuuksia

Tarkastele akun dimensioiden ja materiaalien vaikutusta akun kapasiteettiin
Tarkastele eri ajostrategioiden vaikutusta tuottoon
Syvennä ymmärrystä lämpöakun toiminnasta, tarvittavista säädöistä, käyttömahdollisuuksista,

Tulosten tarkastelun apuvälineitä

Keskeiset suureet piirretään ajan funktiona
Eri parametreilla suoritettujan simulaatioiden tulosten ero prosentteina piirretään ajan funktiona
Lämpötilaprofiili ajan funktiona 3D-animaationa
Tunnuslukuja
- Antamalla tyypillisen vuorokauden sähkön ja kaukolämmön hinta tunneittain, voidaan vertailla tuottoja eri ajostrategioilla ja akun parametreilla
- Antamalla erityyppisten vurokausien sähkön hintaprofiileja, voi kokeilla, millaisia ominaisuuksia akulla ja säädöillä olisi hyvä olla

Physics (Governing Equations)

Problem: A 2‑D axisymmetric solid heat store (in cylindrical coordinates $r,z$) is coupled to a 1‑D plug‑flow fluid in a pipe running along the axis. Heat exchange at the pipe wall is modeled with a convective (Robin) boundary condition.

Coordinate convention: x = z (axial), y = r (radial). No $\theta$ dependence (axisymmetry).

Geometry and material parameters

Solid annulus: $ r \in [R_{\text{pipe}},,R_{\text{solid}}], z \in [0,,L]$
Pipe radius $R_{\text{pipe}}$, outer solid radius $R_{\text{solid}}$, length $L$
Solid properties: density $\rho_s$, heat capacity $c_s$, conductivity $k_s$
Fluid (oil) properties: density $\rho_f$, heat capacity $c_f$
Convective heat‑transfer coefficient at the wall $h$
Reference temperature $T_{\text{ref}} = T_{\text{initial}}$

All quantities are in SI units.

Solid (axisymmetric heat equation)

\[ \rho_s c_s\,\partial_t T_s = \nabla\!\cdot\!\big(k_s \nabla T_s\big), \quad (r,z)\in \Omega. \]

Axisymmetric Laplacian (no $\theta$):

\[ \nabla\!\cdot\!(k\nabla T) = \frac{1}{r}\,\partial_r\!\big(r\,k\,\partial_r T\big) + \partial_{zz}(k T). \]

Boundary conditions

PIPE wall $r = R_{\text{pipe}}$ (convective exchange to the fluid): \[ -k_s\,\partial_n T_s = h\,(T_s - T_f^\ast), \] where $T_f^\ast(t,z)$ is the fluid temperature interpolated along the PIPE boundary.
Outer wall $r = R_{\text{solid}}$: typically insulated, \[ \partial_n T_s = 0 \]
Ends $z = 0, L$: typically insulated,

\[ \partial_n T_s = 0 \]

(adapt if you model end losses).

Fluid (1‑D energy along the pipe)

\[ \partial_t T_f + v\,\partial_z T_f = \alpha_{\text{eff}}\,\partial_{zz} T_f + \beta\,(T_w - T_f), \quad z \in (0,L). \]

Plug velocity $v$ (m/s).
Axial “artificial” diffusivity $\alpha_{\text{eff}}$ (often $=\alpha_f$, can be 0).
Wall‑exchange coefficient $\displaystyle \beta = \frac{2h}{\rho_f c_f R_{\text{pipe}}}$.
$T_w(t,z)$: segment‑average of the solid wall temperature at the PIPE.

Fluid boundary conditions

Inlet $z=0$: Dirichlet $T_f(0,t) = T_{\text{in}}(t)$ (controller).
Outlet $z=L$: natural outflow for advection; Neumann for diffusion, $\partial_z T_f = 0$.

Energies and powers (full 3‑D via axisymmetry)

Solid internal energy (J): \[ E_{\text{solid}} = \int_{\Omega} \rho_s c_s \,\big(T_s - T_{\text{ref}}\big)\, (2\pi r)\, d\Omega. \]
Oil internal energy (J): \[ E_{\text{oil}} = \int_{0}^{L} \rho_f c_f \,\big(T_f - T_{\text{ref}}\big)\, A \, dz, \quad A = \pi R_{\text{pipe}}^2. \]
Wall power (solid side) (W): \[ Q_{\text{wall}} = \int_{\Gamma_{\text{pipe}}} h\,\big(T_s - T_f^\ast\big)\,(2\pi R_{\text{pipe}})\, d\Gamma. \]
Inlet power (W): \[ P_{\text{in}} = \rho_f c_f \, v\, A \, \big(T_{\text{in}} - T_{\text{ref}}\big). \]

Numerics (Discretization & Algorithm)

Mesh and coordinates

The solid (r–z) domain is meshed in Gmsh (transfinite; optional grading grad in r and bump in z, quads or tris).
The PIPE boundary carries a tag "PIPE"; its edge segments define the fluid grid: the fluid nodes z are taken from the PIPE segments (segment endpoints → nodes).

Solid discretization (Gridap FEM)

Space: continuous $H^1$, P1 Lagrange elements on the 2‑D axisymmetric mesh.
Axisymmetric integration weights:
- domain weight $w_\Omega(x) = 2\pi x[\text{RADIAL}] = 2\pi r$,
- PIPE weight $w_\Gamma = 2\pi R_{\text{pipe}}$.
Time discretization: θ‑method with θ = 1 (implicit Euler). For test $v$ and trial $u$: \[ a(u,v) = \int w_\Omega \left(\frac{\rho_s c_s}{\Delta t}\,vu + \theta\,k_s\,\nabla v\!\cdot\!\nabla u\right) d\Omega + \int \theta\,h\, w_\Gamma\, v u \, d\Gamma, \] \[ \ell(v) = \int w_\Omega \frac{\rho_s c_s}{\Delta t}\, v\,u^{n} \, d\Omega + \int \theta\,h\, w_\Gamma \, v\, T_f^\ast \, d\Gamma. \]
The left‑hand side is time‑invariant → assemble once, compute a CHOLMOD Cholesky factor, and reuse each step.

Fluid discretization (1‑D FV on non‑uniform z)

Control volumes centered at nodes; half‑cells at ends $i=1,N$.
Face advection flux (upwind): \[ F^{\text{adv}}_{i+1/2} = v \, T^{\text{upwind}}. \]
Face diffusion flux: \[ F^{\text{diff}}{i+1/2} = - \alpha_{\text{eff}} \frac{T_{i+1}-T_i}{\Delta z_{i+1/2}}. \]
Explicit conservative update for interior nodes: \[ T_{i}^{n+1} = T_i^n + \Delta t \left[ -\frac{F^{\text{adv}}_{i+1/2}-F^{\text{adv}}_{i-1/2}}{\Delta z_i^{\text{cv}}} -\frac{F^{\text{diff}}_{i+1/2}-F^{\text{diff}}_{i-1/2}}{\Delta z_i^{\text{cv}}} + \beta (T_{w,i} - T_i^n) \right]. \]
Outlet $i=N$: right diffusive flux set to 0 (Neumann); advection uses upwind.
Inlet $i=1$: Dirichlet $T_1 = T_{\text{in}}(t)$.

Coupling (staggered explicit per time step)

Inlet: set $T_f(0,t)$ from the controller (based on $T_{\text{out}}$ and/or time).
Interpolate fluid to PIPE: build a boundary CellField $T_f^\ast(z)$ on "PIPE" from the current T_f.
Solid step: solve the implicit Euler system with the cached factorization → get $T_s^{n+1}$.
Wall temperature for fluid: compute $T_w(z)$ as segment‑averages on "PIPE": exact L² projection onto a P0 boundary space (diagonal solve), then sample at segment midpoints and map to nodes.
Fluid step: explicit FV update to $T_f^{n+1}$ with upwind advection, optional $\alpha_{\text{eff}}$, and exchange $\beta(T_w-T_f)$.
Audits: $E_{\text{solid}}, E_{\text{oil}}, Q_{\text{wall}}, P_{\text{in}}$, cumulative balances.
Output: VTK for solid (unstructured) and fluid (rectilinear r–z grid).

Stable time step

On a non‑uniform grid, the step is limited by the tightest local constraint: \[ \Delta t \le \min_i \Bigg( \text{CFL}_{\text{adv}}\frac{\Delta z_i}{|v|},\; \text{CFL}_{\text{diff}}\frac{\Delta z_i^2}{\alpha_{\text{eff}}+\varepsilon},\; \text{CFL}_{\text{xchg}}\frac{1}{\beta} \Bigg). \] Your implementation computes this once from z and params (with conservative defaults).

Energy accounting (axisymmetric 3‑D)

Solid energy $E_{\text{solid}}$: FEM integral with weight $2\pi r$, relative to $T_{\text{ref}}$.
Oil energy $E_{\text{oil}}$: trapezoid on z times cross‑section $A$.
Wall power $Q_{\text{wall}}$: Robin term integral on "PIPE" with weight $2\pi R$.

All audits use the same measures as the solver to keep units and geometry consistent.

Tehtävää

Menetelmän dokumentointi

Tämän dokumentin viimeistely.
Koodin kommentoinnin täydentäminen

Validiointi ja verifiointi

Toistaiseksi lasketaan energiataseen virhe. Mallissa ei ole lämpövuotoja, joten sisään syötetyn energian ja varastoituneen energian pitää olla samat.
Ajan funktioita ja animaatiota tarkastelemalla voi silmämääräisesti arvioida tulosten järkevyyttä
- Kokeilemalla mallia laajalla parametrien arvoalueella on varmistettu mallin robustiutta
Tärkeä tieto on nopeus, jolla akku kykenee vastaanottamaan ja luovuttamaan lämpöä. Tähän ominaisuuteen ei ole yhtä yksinkertaista tarkistusta kuin energian säilymiseen.
Tekoälyn avulla pitää kehitellä keinoja varmistaa mallin riittävä tarkkuus
Mikäli johonkin koelaitokseen asennetaan lämpötila-antureita, ne antavat arvokasta tietoa mallin verifiointiin sen lisäksi, että auttavat arvioimaan akun varaustasoa.

Paketointi yleiskäyttöiseksi

Tähän ei kannata ryhtyä ennen kuin joku taho haluaa vakavissaan tätä työkalua käyttää.

Ohjeet julia-ohjelmointiympäristön installointiin ja päivittämiseen. Suoraviivainen homma, mutta vaatii työtä
Julia-projektin paketointi helposti installoitavaksi. Projekti sisältää määrittelyn tarvittavista kirjasto-ohjelmista, simulointiohjelman ja komentotiedostoja yms.
Käyttöohjeita pitää kirjoittaa.
Käytettävyyttä pitää parantaa, vaikkei graafista käyttöliittymää tekisikään

3D simulointi

Samalla periaatteella kuin 2D malli voidaan laatia 3D-malli lämpöakun lohkosta. Periaatteessa tekoäly osaisi melko suoraviivaisesti muokata nykyisestä 2D mallista 3D mallin. Yksi haastava vaihe olisi muodostaa lohkon laskentahila.

2D mallia laadittaessa tekoäly teki monen tasoisia virheitä, vääriä johtopäätöksiä ja huonoja valintoja, joiden selvittely ja korjaaminen vei aikaa. Samaa olisi odotettavissa 3D mallia laatiessa.

3D malli vaatisi laskentatehoa moninkertaisesti 2D malliin verrattuna. Läppärin teho ei riittäisi.

Lisähyöty olisi rajallinen.